The term degrees of freedoms is most widely used in various fields like statistics, machine tools, mechanisms, vibration, FEM, etc. Whatever the field, the number of degrees of freedom can be defined as the minimum number of independent coordinates that can specify the position of the system completely.
Especially in FEA DOFs has greater importance due to the fact that, FEA simulation solution (time) depends on number of degrees of freedom of the system to be analyze. We will discuss at the end how DOFs affect the solution time.
Let’s discuss Simple problem to understand the concept of DOFs.
Refer Figure 1, the point force is acting at the end of the rectangular beam, Due to downward load application, the beam will deformed to new position, consider the particles in small color region at end of beam and try to identify the location of particles for the new deformed position. Can we say that, we can solve this problem? We can say yes, if we are able to define the new position (deformed position) of each and every particle of the beam. So how do we get that? We will get the deformed position, only after identifying the number of parameters to define the new position from existing one. We will need coordinates in different planes, respective angles and distances from the origin, etc. then only we are able to define deformed position.
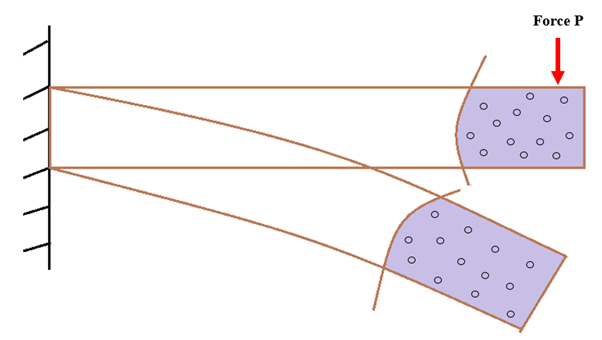
The minimum number of parameters (motion, coordinates, temperature, etc.) required to define the position and state of any entity completely in space is known as degrees of freedom (dof).
Furthermore, let’s discuss DOFs through 1D, 2D and 3D space problems.
1D Space DOFs:
Let’s start with simpler 1D space which will be easier to understand. There are very limited uses of 1D in FEA…in fact that, it is only used to tally the FEA results with hand calculations. 1D space consist only 1 dimension and hence the matrices are small resulting quicker solution to the problems.
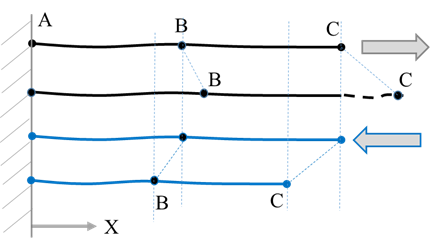
- Figure 2 shows the string, which is fixed at one end (Point A) and force is applied at other end on point C. The force is acting on point C in one direction; when pull force acts the point C shifts in positive X direction, if push force acts the point shifts in negative X direction. Point B is share elements between A & C of the string. So once force is applied on C, the point B elements are either elongate or shorten in X axis. It means point B or C position can be identified with one information (deformation along axis X) only, means this is a 1 DOF system. So in case of 1D space, only 1 dimension means 1 DOF is enough to define the position.
2D Space DOFs:
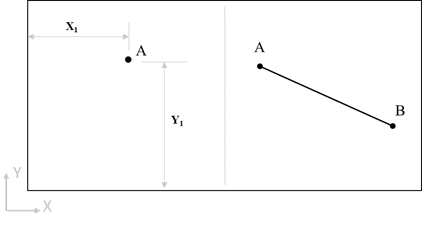
Now let’s discuss about 2D space, when we talk about 2D space, movement can be possible in two directions. Figure 3 shows the point A in 2D planer problem, here in order to define the position of point A completely with respect to origin, you need two parameters i.e. X1 & Y1, it means two dofs (translation X & Y). Suppose if point A is part of line (line AB), in such case you will also need one angle to define along-with two translations i.e. 3 dofs (two transnational and one rotation).
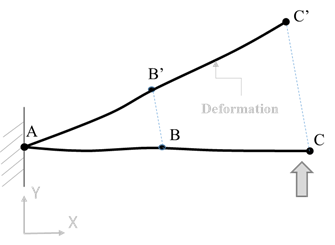
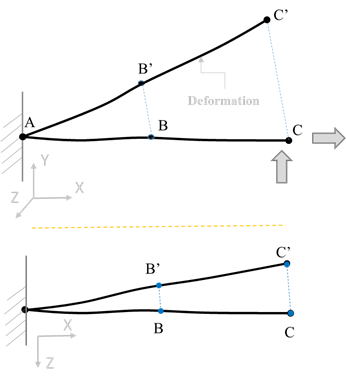
- Let’s consider same string problem in 2D space FEA, Figure 4 shows string with point A is fixed and vertical load is applied on point C. The vertical loads on point C causes the string to deform upwards to new position B’-C’. The new deformed position of the string B’-C’ is happened because of movement along axis X, Y and in plane rotation (it would about Z Axis).
3D Space DOFs:
3D space is more realistic and accurate environment for FEA as most of problems lies in 3D space. Now suppose the line AB is rotated arbitrarily with respect to origin and shifted out of the plane is as shown in Figure 5. Here in 3D space, to define the position of point A or any point on line AB, the minimum number of parameters would be 6 DOFs, i.e.3 transnationals (Ux, Uy, Uz) & 3 rotations (Rx, Ry, Rz).
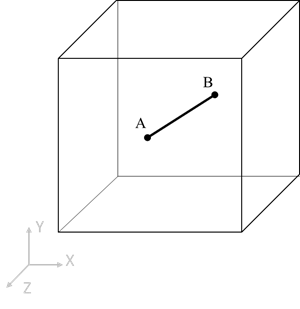
- Let’s consider further same string problem in 3D space with vertical & additional axial force application at the end of string which causes the string to deformed to new position B’-C’. This deformed position is achieved not only in single plane but also two mutually perpendicular planes too (means in all three planes). Check Figure 6 for deformed position in XY from front side and XZ plane from top side, similar string will have some movement in YZ plane too. It means that, if want to defined the position of any point or node of string, you would need minimum three transnational and three rotational coordinates, i.e. 6 dofs.
Now you might understood the concept of degrees of freedom. But as mentioned earlier the FEA solution time depends on total number of dof of the system to be analyze, but How?
As we know that, any object or component have infinite number of points and you use FEA to convert infinite to finite ( limited number) of points with the help of discretization for analysis. Discretization i.e. meshing is used to create finite points as elements and elements forms nodes at joining. But all elements does not have 6 dof per node. The number of dofs depends on the type of element (1D, 2D, 3D), the family of element (plane stress, plane strain, membrane, thin shell, etc.), and the type of analysis. For example, for structural analysis of vessel, a solid elements has 3 dof/node (3 transnational) while if you use shell elements at mid-surface may have 6 dof/node (3 rotational and 3 transnational) and if you do thermal analysis of shell, you will have only single dof/node. For beginner, it is quite confusing but once you will practice, will understand the logic’s behind specific number of dofs to different elements and analysis types.
- Let’s consider small portion of rectangle as shown in first sketch of figure 7, the total number of point within selected region are infinite and have 6 dofs/nodes, the equations formed in this case are ( ∞ X 6) infinite and hence it is required to convert finite points to infinite numbers with the help of mesh, refer sketch 2 with 12 elements and 15 nodes, the equations formed here are only (6 x 15) are 90. Furthermore, third sketch shows the solid mesh which haves only 3 dof per nodes which gives (27 X 3) 81 equations for calculations.
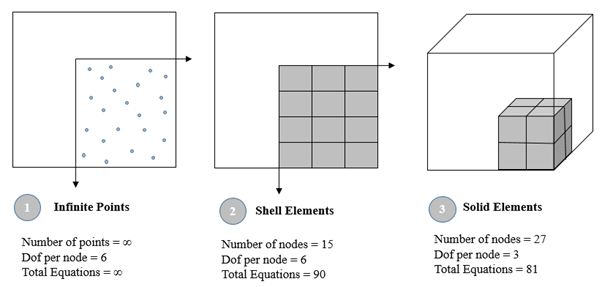
Thus it concludes that DOF is a very important concept. In FEA, we use it for the individual calculation points (used to solve partial differential equations). The total DOFs for a given mesh model is equal to the number of nodes multiplied by the number of dof per node. More the number of dofs, higher the equations & large solution time.
